![]()
NURBSボリュームの作り方
2025.05.15
パラメトリック・ボイス
コンピュテーショナルデザインスタジオATLV 杉原 聡以前のコラムで記したように、3月に東京大学で開催された国際学会CAADRIA2025にて筆者
はM. C. エッシャーとNURBSボリュームをテーマとしたワークショップを開催した。NURBS
ボリュームとはNURBS曲面の定義を1次元追加して、密度を変えながら湾曲する直方体を定義
し、その内部で湾曲と密度に応じた位置を計算できるようにしたNURBSジオメトリーの一種
である。あまり聞かないジオメトリーであるが、NURBS曲線を実装してからNURBS曲面を実
装すると、もう1次元分処理を追加すればNURBSボリュームが可能になることが容易に分かる。
そこで今回はNURBSボリュームの作り方について記す。
まずはNURBS曲線から話を始める。NURBS曲線を定義するのに必要な情報は、制御点の配列、
制御点と同じ数のウェイト(4次元の点x, y, z, wを制御点に使ってそのw要素をウェイトとす
ることが多い)、曲線の次数(degree)、単調増加する小数の配列であるノットベクトルである。
あと開始パラメータ値と終了パラメータ値を要することもあるが、通常はノットベクトルの最
初の値と最後の値に一致する。また、デフォルトのノットベクトルであれば制御点の数と次数
から生成できる。
これらの情報、特に制御点から定義されるNURBS曲線は、基本的には制御点の間を補間した曲
線である。最も単純な補間は2つの制御点から定められる直線を考えれば良い。図1のように制
御点p1、p2があるときに、この2つの点を始点と終点とする直線は、その間で0から1に変化す
るパラメータuによって線形補間(ベクトルp1、p2のuによる重み付き和)によって直線上の
点C(u)が定義され、直線そのものはその点の集合として定義される。
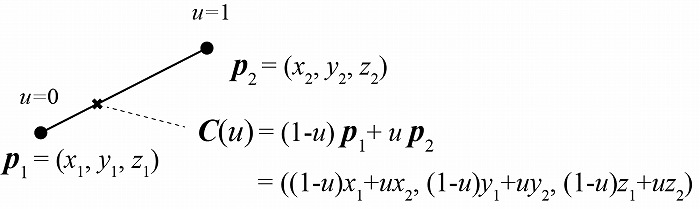
図1 2点の線形補間
このとき、uに応じたp1の比率とp2の比率は図2aのグラフのように表され、u=0の最初はp1
の比率(赤)が1で p2の比率(水色)が0、u=0.5でそれぞれ半々になり、u=1.0で0(赤)と1(水色)
になり、直線の位置がp2と一致する。また制御点が4個の折れ線の場合は、図2bのグラフのよ
うに制御点と制御点の間でそれぞれの隣接する点との補間が起きている。
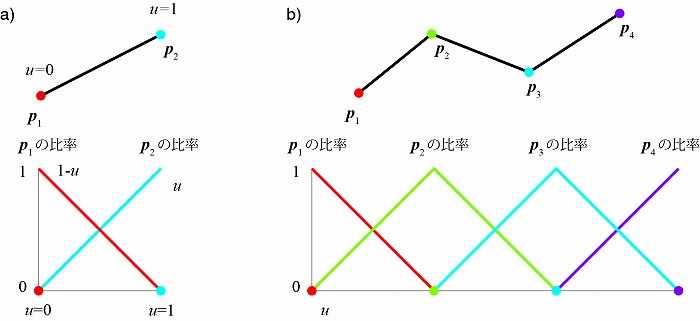
図2 2点の直線の補間の比率
ところで、NURBS曲線の定義に要する情報で最も聞き慣れないものはノットベクトルである
と思われるが、これは0, 0, 1, 2, 3, 3のような単調増加する小数の数列であり、これを用いて
基底関数を定義する。その基底関数とは何かと言うと図2で示されたグラフのような複数の制
御点の補間の比率を表す関数である。図2の直線や折れ線上の位置は、端点や角を除き2つの制
御点の補間で定められている。それが2つではなく、3つ以上の制御点の補間で線上の位置が定
められるのが次数2以上のNURBS曲線であり、直線的ではなく曲線となる(図3)。ちなみに図2
の直線と折れ線もNURBS曲線として定義され、その次数は1である。NURBS曲線の基底関数は
区分多項式関数であるバーンスタイン多項式で表され、その多項式の最大次数はNURBS曲線の
次数と一致する。次数が2である図3aの基底関数は2次多項式で表され、曲線上の位置は隣接す
る3つの制御点の補間で定められる。同様に図3bの次数が3のNURBS曲線の基底関数は3次多項
式で表され、隣接する4つの制御点の補間で位置が定まる。
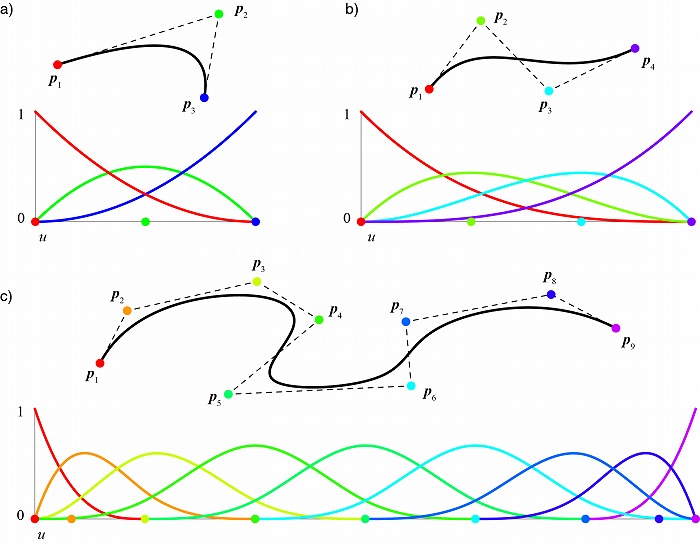
図3 NURBS曲線と基底関数a)次数2、b) c) 次数3
また、制御点ごとに定められたウェイトは、円や弧を定める際以外はあまり用いられないが、
制御点を補間に用いるときに掛け合わされて、制御点の曲線への影響を調整する(図4)。
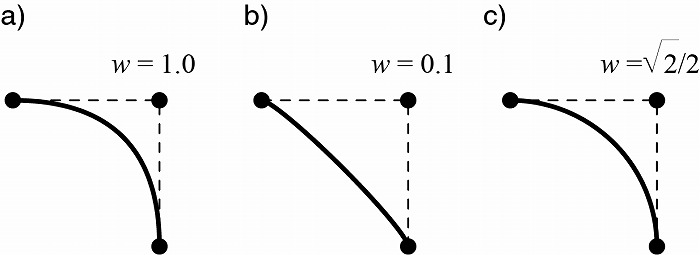
図4 NURBS曲線のウェイト(cは90°の弧)
曲線上の位置を定めるパラメータuは、図2aでは0から始まり1で終わっていたが、必ずしもそ
うとは限らない。なお、Grasshopperにて曲線や曲面の入出力値にReparameterizeオプショ
ンを指定することがあるが、これは開始パラメータ値と終了パラメータ値を0と1に再計算する
ことを意味する(それに伴いノットベクトルとそこから計算される基底関数も再計算される)。
以上の情報を用いて、曲線上の点が計算される。Grasshopper上では、Evaluate Curveコン
ポーネントがその計算を行っているが、この計算さえできれば曲線の描画や分析など大半のこ
とが計算可能となる。曲線の接線も微小に間を開けた2点のベクトル差から計算できるが、よ
り正確に計算するには点の位置を計算する式をuについて微分した式を用いると良い。制御点
はuで変化しないため、区分多項式である基底関数を微分して求められる多項式を用いれば接
線ベクトルは正確に計算できる(詳しくは下記の筆者の実装を参照)。
では次にNURBS曲面についてである。NURBS曲面の定義に必要になる制御点は、曲線の1次
元配列に代わり、U方向とV方向の2次元配列になり(ウェイトは4次元ベクトルのwとして各制
御点に含むこととする)、次数やノットベクトルもU、Vそれぞれについて2種類定められる。例
えば図5では、3×4の制御点で定められるU方向の次数は3、V方向の次数は2のNURBS曲面が
描かれている。
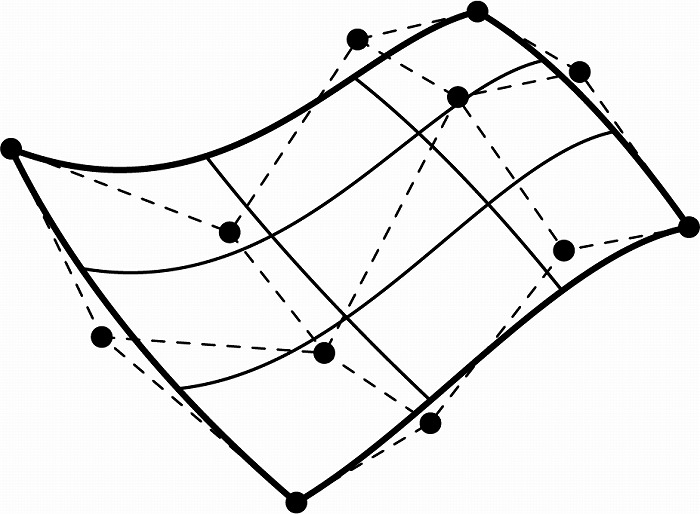
図5 NURBS曲面
曲面内部ではU、Vについての2つの基底関数が計算され、それらを掛け合わせた値と、U、V両
方向における近傍の制御点を用いた補間によって、曲面上の点の位置が計算される。接線ベク
トルの計算もNURBS曲線と同様に、UとV方向の基底関数を微分したものを用いて計算でき、
法線ベクトルはU方向の接線ベクトルとV方向の接線ベクトルの外積によって導かれる。
さて最後にNURBSボリュームについてである。制御点は曲面において2次元配列としたのと同
様に、U、V、W方向の3次元配列とすれば良い。次数やノットベクトルもU、V、Wそれぞれに
ついて合計3種類定められる。例えば図6は5×4×4の制御点で定められる、U、V、W方向の次
数が全て3のNURBSボリュームである。基底関数もU、Vに加えてWの3つが定められ、u, v, w
パラメータで指定されるボリューム内の点の位置が、これらの基底関数を掛け合わせた値と3つ
の方向で近傍の制御点を用いた補間で計算される。U、V、W方向の接線ベクトルも上記と同様
にそれぞれの基底関数の微分を用いれば良い。
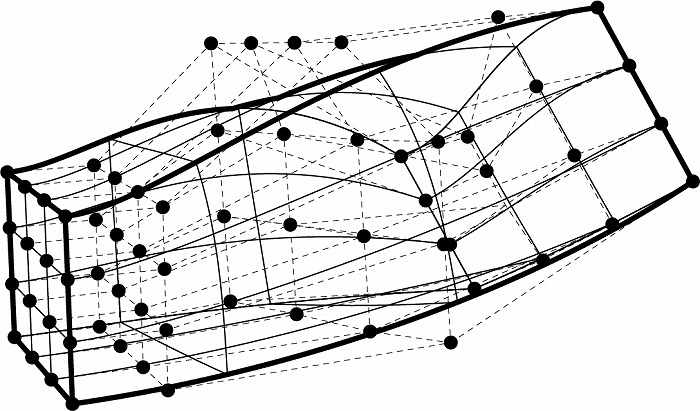
図6 NURBSボリューム
と言う訳で、一度NURBS曲線に必要な仕組みが揃えば、NURBS曲面やNURBSボリュームを実
装するのはそれほど煩雑ではなく、制御点を多次元化し、他の要素を次元が増える分追加する
だけでできてしまうのである。同じ手順で、NURBS4次元ボリューム、NURBS5次元ボリュー
ムなど実装もできるはずであるが、ただ2Dまたは3Dグラフィック表示のための2次元または
3次元への投影の処理は上手く考える必要があるであろう。NURBS曲線、曲面、ボリューム、
4次元ボリュームと区別せず、NURBS n次元ジオメトリーを実装している人もいると聞く。
NURBS曲線、曲面、ボリュームの実際の実装に興味のある方は、Processing用のコンピュテー
ショナルデザインライブラリとして私が開発しているiGeoのソースコードをご覧いただけたら
と思う。
・NURBS曲線の実装:ICurveGeo
曲線上の点の位置の計算はvoid pt(double u, IVec retval)メソッドで、接線の計算はvoid
tan(double u, IVec retval)メソッドでなされている。
・NURBS曲面の実装:ISurfaceGeo
曲面上の点の位置の計算はvoid pt(double u, double v, IVec retval)メソッドで、接線の
計算はvoid utan(double u, double v, IVec retval)メソッド、void vtan(double u,
double v, IVec retval)メソッドでなされている。
・NURBSボリュームの実装:IVolumeGeo
ボリューム内の点の位置の計算はvoid pt(double u, double v, double w, IVec retval)
メソッドで、接線の計算はvoid utan(double u, double v, double w, IVec retval)メソッ
ド、void vtan(double u, double v, double w, IVec retval)メソッド、void wtan(double
u, double v, double w, IVec retval)メソッドでなされている。
また、NURBSボリュームを作ってはみたが、これは何に使うのか?という問いは、未だ答えが
定まっていない開かれた問である。1つの使い道としては、NURBS曲面から構造の生成やパネ
ル化を行うように、NURBSボリュームからそのボリューム内部へまとめて構造の生成やパネル
化、そして小さいボリュームへの分割(セル化、cellularizationと筆者はひとまず呼んでいる)
をするという利用法がある(図7)。筆者がCAADRIA2025で行ったワークショップもこれら
のスタディーについてであった。ワークショップの内容についてはまたの機会とするが、ワー
クショップで使ったNURBSボリュームのチュートリアル用コード例のページは公開されている
ので以下にそれを紹介して今回のコラムを締める(図8)。
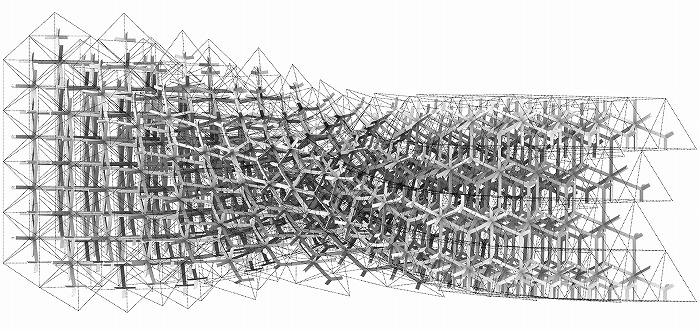
図7 NURBSボリュームからの構造ジオメトリー生成

図8 iGeoにおけるNURBSボリュームのセル化チュートリアル例
※上記の画像、キャプションをクリックするとNURBSボリュームのチュートリアル用
コード例のページへリンクします。